Reinforcement Learning applied to Learning Beast Behaviour

The simplest (effective) such techniques seem to use the idea of temporal difference; of these, Q-learning is straightfoward and has some nice convergence properties.

There are two aspects to these algorithms:

• The process of learning the control policy itself, which is essentially a mapping from world-states to actions that result in the maximum reward over the long term.
• Selection of an action, given a world-state. While learning, there is a need to trade off exploitation versus exploration.

Q-Learning

The update rule is as follows:
Q(s, a)' := Q(s, a) + alpha * (reward + gamma * max_a'[Q(s', a')] - Q(s, a))
where:

• s: the current state.
• a: the action taken, resulting in new state s'.
• alpha: learning constant (0.1).
• gamma: the discount on future rewards (0.9).
• reward: the reward for making action a in state s, resulting in state s'.

Note that it may be the case that the successor state is not entirely determined by the action performed by the agent.

The formula can be applied directly, in a forward manner; this is nice as the memory requirements are low. The problem is that learning is quite inefficient, given the usual "zero rewards mostly" learning scenario, as non-zero rewards will only be propogated backwards very slowly.

The alternative is to maintain a stack of (state, action, reward) triples, and update the Q-values at some convenient time backwards, i.e. from most-recent reward to the bottom of the stack.

The requirements for the algorithm to converge on a optimal control policy are as follows:

• Deterministic Markov process (this is probably not the case here.)
• Bounded reward function.
• Each (state, action) pair is visited infinitely often.

See [Mitchell] for details.

Action Selection Policies

• e-greedy: Select the action with the highest Q-value (1 - e) of the time ("greedy"), and a random one e of the time. Note this doesn't factor in the relative merits of any actions except the one with the largest Q-value.
• softmax: Add a random number drawn from a long-tailed distribution (e.g. a normal distribution with x >= 0) to each Q-value, and select the largest. Additionally, a temperature may be factored in so that exploration is encouraged early on, and exploitation used later.

  The problem with the first approach is that the random numbers must be commensurate with the Q values, which cannot be a priori guaranteed with a fixed scaling factor. The solution is to go with the stock Gibb's distribution:

  p_j = e^x_j / sum_{i in 1..n} [e^x_i]

  where p_j is the probability of choosing action j in a particular state.

Learning Beast Behaviour

• State space: 8 immediately adjacent squares (blocked or empty: everything except Player is mapped to "blocked"), 3x3 vector to the player (-1, 0, 1), distance (adjacent, near, far).
• Action space: move in one of the 8 dirs. Staying still is probably not that exciting.
• Exploit symmetry in the state space: rotate the state so that the player is always "North" of the beast in the transformed space. then: "y" is one of {near, far}, "x" {left, middle, right}. Choose the longest component of the player vector for the "straight ahead" bit, shortest for the tranformed x co-ordinate.

  Use a big flat array: index it with location (8 bits), "y" (2 bits), "x" (3 values, so 2 bits). Thus the state space has 1536 different configurations. Using something like Q learning, this uses 9 (actions) * 1536 * 4 (bytes/float) = roughly 56k of memory.

  Encode states to ints:

  • lower 8 bits are the blocks in adjacent squares (0 == empty (player, empty space), 1 == blocked (everything else)).
  • next bit is the distance ({near, far}).
  • next 2 bits are the direction vector (squashed to {left, middle, right}).

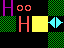  Rotated 90 degrees anti-clockwise (so that the player is directly "north"), with all objects squashed to the set {0, 1} as above, results in:

• Reward function:
  • Invalid move: -1000 (immediate)
  • Dying: -5.
  • Moving towards the player (NW, N, NE in the transformed space): 2.
  • Kill player: 10

  Delay giving the beast the reward until the next time it moves.

Pragmatics

• No need to pre-process the value-action table for e.g. invalid moves: let it learn them by retrying on invalid move.
• [Sutton and Barto] suggest: To encourage exploration early on, initialise the value-action table with wildly optimistic values. All Q-values are way too high, and so even the good moves result in smaller-than-initial Q-values. Note this is only a partial solution to the exploration versus exploitation problem; I have abandoned this as it seems unnecessary.
• Special case: if we're adjacent to the player, only one move makes sense: move towards it!

References

[Sutton and Barto] Richard S. Sutton and Andrew G. Barto, Reinforcement Learning: An Introduction, MIT Press, 1998.

Thanks to Waleed for several discussions, and in particular, the formulation of the state-space transformation.