Next: About this document ...
Up: COMP9417 Project Shapiro's Model
Previous: Bibliography
Logic and Logic Programming Definitions
Most of these definitions follow Lloyd [Llo87b].
Unconstrained resolution, while an improvement on its predecessors, is
still a massively non-deterministic search through a very large space of
possible proofs. Interestingly, there is a class of clauses - the
definite clauses - over which a variant of resolution can be made
quite efficient.
Assume or give a brief overview of most-general-unifiers. A good
overview of resolution theorem proving and its relationship to logic
programming is [Rob92].
- Atom:
- If
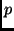 is a predicate symbol and
is a predicate symbol and 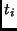 are terms, then
are terms, then
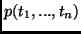 is an atom. Note this is at odds with the builtin
meta-predicates atom and atomic.
is an atom. Note this is at odds with the builtin
meta-predicates atom and atomic.
- Chronological backtracking:
- In Prolog, a failing computation causes a
re-examination of the most-recent choice of the clause to execute, in a
context where there were several alternatives. The computation proceeds
with some other selection.
- Clause:
- A clause is a logical formula in conjunctive
normal form, which has the schema:
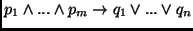 or, equivalently,
or, equivalently,
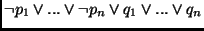 where
where 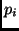 and
and 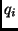 are atoms.
are atoms.
Clocksin and Mellish [CM81, Appendix B] give a Prolog
program to convert arbitrary first-order formulae into clausal form.
- Functor:
- A function symbol/arity pair. These have the same role as
records in other languages (structs in C) which is to aggregate
data. These are the data constructors in the context of type
systems.
- Ground:
- A term or atom is ground if it contains no variables.
- Horn Clause:
- A clause containing at most one positive literal,
written (with the commas interpreted as
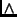 ):
):
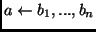 (a definite clause) or
(a definite clause) or
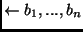 (a
definite goal). Note that introducing negated body goals into the
language violates this definition.
(a
definite goal). Note that introducing negated body goals into the
language violates this definition.
- Instance of:
- One term is an instance of another if it is more
instantiated than it, in the sense that it is the result of applying
some substitution to the other.
Formally: 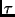 is an instance of
is an instance of 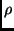 if there exists a substitution
if there exists a substitution
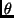 such that
such that
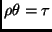 , written
, written
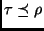 .
.
- Mode:
- instantiation states - i.e. whether a variable is bound or
free, or in terms of predicates, whether an argument position is an
input or an output (or both). Note that the instantiation
state of a term can be arbitrarily complex.
- Module System:
- Some mechanism for dividing a program into separate
compilation units, for the purposes of abstraction.
- Negation-as-finite-failure:
- Prolog uses the
closed-world-assumption: if it cannot prove a goal using the
clauses in it's database, and the proof attempt fails after a finite
number of steps, then the goal is deemed to be false. This rule means that
Prolog implements a non-monotonic logic: it is not necessarily the
case that adding more clauses to the theory will lead to more things being
provable. This is in contrast to classical first-order logic, which is
monotonic.
- Predicate Symbol:
- A predicate symbol is a string/arity pair
that names a set of clauses (all of which have the same predicate symbol
as heads).
- Pure Prolog:
- Restriction of the language to Horn clause logic - i.e.
no higher-order constructs (call/1, findall/3, ...),
meta-predicates (functor/3, arg/3, ...) or built in
arithmetic (is/2, ...).
- Resolution:
- A sound and complete proof technique for first-order
clausal logic, invented by Robinson in the early 1960's
[Rob92]. Prolog uses a variant of full resolution, where
constraints are imposed on clauses and the inputs to the resolution step,
called SLD-NF resolution (linear resolution over definite clauses with a
selection function, combined with the non-monotonic negation-as-failure
rule [Llo87b]).
- Substitution:
- A substitution is a function that maps a set of
variables to a set of terms, and is usually denoted
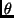 . We write
. We write
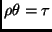 to indicate that the term
to indicate that the term 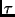 results when we apply
substitution
results when we apply
substitution 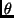 to term
to term 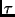 .
.
- Term:
- A term is one of: a variable, a constant symbol (e.g. a
numeral), or a compound structure
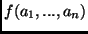 where
where 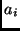 are
terms. In the latter case,
are
terms. In the latter case, 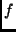 is called a function symbol,
is called a function symbol, 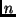 is
the arity of the term, and
is
the arity of the term, and 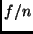 is the functor.
is the functor.
- Type:
- A type is a collection of objects deemed to have some common
property, such as the set of natural numbers.
- Unification:
- Unification can be viewed as a generalisation of pattern
matching (such as that found in Haskell) in that variables can be bound in
both the pattern and the object matched against, rather than just
the pattern.
Unification is used in Prolog for assignment, memory allocation, pattern
matching, argument binding, etc. As such it can be heavily optimised
provided we can discover (essentially) mode information.
More formally, we assume the existence of a sound method of finding the
most general unifier (mgu) of two terms, written
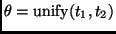 . See [Llo87b] for more details.
. See [Llo87b] for more details.
- Variants:
- Two terms are variants if they are identical modulo
a variable renaming, which is analogous to
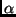 -convertibility in the
lambda calculus.
-convertibility in the
lambda calculus.
If 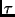 and
and 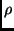 are variants, we write
are variants, we write
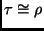 . Obviously
. Obviously
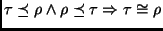 .
.



Next: About this document ...
Up: COMP9417 Project Shapiro's Model
Previous: Bibliography
Peter Gammie
2002-03-01
![]() is an instance of
is an instance of ![]() if there exists a substitution
if there exists a substitution
![]() such that
such that
![]() , written
, written
![]() .
.
![]() . See [Llo87b] for more details.
. See [Llo87b] for more details.
![]() and
and ![]() are variants, we write
are variants, we write
![]() . Obviously
. Obviously
![]() .
.