... trees¹

As distinct from resolution proof trees where the emphasis is on what objects participate in each step of the proof. We elide such details here as the emphasis is on searching through the intermediate (ground) results of a proof to identify faulty clauses in the theory (Section 2).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... language²

Once we allow such objects in the hypothesis space, we have all sorts of computability issues to deal with. For example, it is no longer the case that the process of checking that the theory entails the observations necessarily terminates.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... viewpoint³

Prior to Kant, that is.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... them⁴

Obviously there are plenty of technical caveats if this is to go through: for example, the observations must completely characterise the target set, which is required to be describable in some formalism (in other words, it must be at least recursively enumerable).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

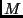...$M$⁵

In less logical language, MIS assumes that the user has an intuitive idea of or can empirically verify the ground facts in 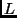$L$. Loosely, the collection of these facts is termed a model, and the point of this exercise is to find a set of clauses that describes the model.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... way⁶

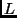Indeed, if a theory contains a contradiction then it contains every statement in $L$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.