Subsections

• Multiple Predicate Learning
• MIS Against FOIL

Conclusion

Having presented Shapiro's Model Inference System, we can now address some of the questions posed in the introduction:

• Why use a logic-based hypothesis language, rather than ones with other, perhaps simpler, semantic foundations?

  An immediate, if partial, answer to this is that logic has a very simple and regular semantics which is intimately reflected in it's syntax. This is exemplified in Section 3, where ``refinement'' is characterised by a simple syntactic criterion.

  In terms of the error diagnosis tools, pure Prolog has the advantage that it only has one way of getting work done: viz, unifying a goal with the head of a clause. Combined with the lack of side-effects, this implies that we can think about predicates purely in terms of their input/output behaviour. In other words, we can (mostly) treat predicates as black boxes and only unfold those that are known to be buggy. This is in contrast to C, where the presence of side-effects allow the source of a bug to be syntactically quite distant from where it manifests.

  Finally, for the purposes of the Model Inference System itself, adding or removing definite clauses have a predictable and incremental effect on a theory. Again, this follows from the simple proof-theoretic semantics of pure Prolog.

• How onerous is the requirement for an oracle for the learning domain?

  The most obvious atypicality of MIS is its reliance on an oracle for the concept it is trying to induce in addition to the training dataset. While this requirement is perfectly reasonable for abstract symbolic domains (such as inducting grammars of programming languages or axiomatising mathematical theories), it fails dismally when the domain has an a priori unknown structure. Concretely, this implies that MIS and indeed any supervised learning technique would be completely useless for, e.g., inducting a grammar for whale songs [Ric00].

• Can MIS be extended to handle noisy data?

  The presence of noise in the training data implies that there will be some overlap between the sets of positive and negative data. As first-order logic does not pretend to deal with contradictions in a very sophisticated way⁶, it is not at all obvious how to retain the logical properties so effectively exploited by MIS in their presence.

• Can MIS scale to interesting learning tasks?

  MIS must make efficient use of the oracle if it is to induce larger-than-toy programs. As our implementation is quite naive and resource-hungry on even small examples, we have no empirical data on this front.

  The other issue that needs to be addressed is limiting the exponential growth in the refinement graph so that interesting programs can be induced in a reasonable amount of time. One way of doing this is to introduce meta-information such as type and mode annotations for the predicate and function symbols in 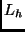$L_h$. Biasing the search almost always leads to incompleteness, which can be problematic.

These last three issues indicate that we must go beyond pure classical first-order logic to find a learning algorithm usable on practical, non-trivial domains. The most obvious recourse is the same as that for the physical sciences: apply statistics. See [MR99] for some recent work on this.

Multiple Predicate Learning

Some concepts cannot be learnt with a single set of clauses that all have the same head symbol (that is, define a single predicate). An example of this is anywhere where two or more levels of recursion (analogous to nested or sequenced loops) are required to express the relation, such as in successor-arithmetic multiplication, and a list-of-lists to lists flattening transformation.

Hence, it is necessary that auxilliary predicates can be introduced. If the learning algorithm can do this automatically, it is said to do predicate invention.

MIS will not create such theoretical terms on it's own initiative, although it can do multi-predicate learning - which is to learn several predicates as part of the one learning task. Additionally, MIS can either learn these predicates concurrently, or learn one and then use it as background knowledge for a later one. In either case, the learning task must be structured, as the oracle must be able to answer queries on every predicate in the target theory.

MIS Against FOIL

FOIL [QCJ93] is a well known ILP system that has quite distinct properties from MIS.

• FOIL uses an incomplete search rule based on a greedy search using the information gain heuristic (in a similar way to ID3, C4.5) to build Horn Clause descriptions of the data.

• MIS is incremental, i.e. a theory is never considered ``finished'' - it can be revised at any time (although the state of the learner needs to be retained). Conversely, FOIL is a bulk, or one-shot learner - give it all the data and it gives you what it considers to be the best description of it.

• MIS uses an intensional check against the facts; it explicitly attempts to prove them using the current conjecture. FOIL uses an extensional covers check while searching for clauses to build a theory from, which is much faster but (even more) incomplete.

• FOIL does unsupervised learning, i.e. there is no need for an idea about what the learnt predicate(s) should look like or what it should do. Conversely, MIS requires that the model being inferred comes equipped with an oracle (something that can evaluate the truth of a predicate at any point in the domain).

• FOIL can handle noisy data, whereas pure MIS cannot.