Next: Examples of MIS Learning
Up: COMP9417 Project Shapiro's Model
Previous: The Contradiction Backtracing Algorithm
Subsections
Refinement
We saw in Section 2 how MIS goes about specialising a
theory that is too general; the counterpart problem of generalising a theory
that is too specific is carried out with the use of a refinement
operator.
The following inputs are required:
- A theory
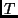 that fails to prove a positive observation
that fails to prove a positive observation 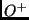 . We
say that
. We
say that 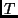 is too-specific; it is incomplete relative to
the concept the oracle has in mind.
is too-specific; it is incomplete relative to
the concept the oracle has in mind.
- An oracle capable of answering queries about the truth of ground atoms
in the model
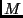 .
.
- A set of marked clauses that the backtracing algorithm has
previously deemed too general to describe
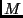 .
.
- A refinement operator, that, when applied to a marked clause,
yields a logically weaker (i.e. more specific) clause.
It should be noted that, even though the new candidate clause is less
general than the previously-considered one, adding it does not decrease
the number of facts entailed by the current theory. (It may not actually
increase it, though.) So, the new conjecture should be considered a
generalisation of the previous one.
Shapiro's generalisation algorithm is parameterised by both the refinement
operator and the strategy that makes use of it. We deal with each in the
following sections.
Refinement Operators
A refinement operator 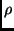 suggests a logically weaker plausible
replacement to a hypothesis refuted by the diagnosis algorithm outlined in
Section 2. Formally,
suggests a logically weaker plausible
replacement to a hypothesis refuted by the diagnosis algorithm outlined in
Section 2. Formally, 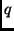 is a refinement of
is a refinement of 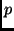 if it
satisfies the following two criteria:
if it
satisfies the following two criteria:
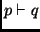 , i.e. everything provable from
, i.e. everything provable from 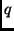 is provable from
is provable from 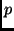 ,
or equivalently,
,
or equivalently, 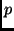 is at least as general as
is at least as general as 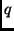 .
.
-
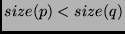 under some size metric. In logic programming
terms, Shapiro uses the following:
under some size metric. In logic programming
terms, Shapiro uses the following:
The 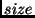 of a sentence
of a sentence 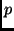 ,
, 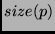 , is the number of symbol
occurrences in
, is the number of symbol
occurrences in 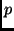 (excluding punctuation symbols) minus the number of
distinct variables occurring in
(excluding punctuation symbols) minus the number of
distinct variables occurring in 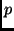 .
.
Intuitively, building a monotonic size increase into the notion of
refinement means that all refinements of 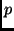 are more specific/weaker than
are more specific/weaker than
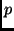 , as it requires more things to be provable (in the case of adding a
body goal) or more structure to be present in the query (if a function
symbol is introduced, or two or more variables are unified). This exploits
the intimate relationship between the syntax and semantics of logic
programs.
, as it requires more things to be provable (in the case of adding a
body goal) or more structure to be present in the query (if a function
symbol is introduced, or two or more variables are unified). This exploits
the intimate relationship between the syntax and semantics of logic
programs.
A refinement operator 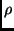 is then defined to be a set-valued function
that maps a statement
is then defined to be a set-valued function
that maps a statement 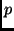 to a subset of its refinements, with some
technical side-conditions.
to a subset of its refinements, with some
technical side-conditions.
A function satisfying this definition induces a partial order (where
``larger'' is interpreted to mean more-specific) over the statements of the
language 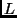 , and can be visualised as a directed acyclic graph (generally
termed a Hasse diagram in the context of partial orders). If all
statements in
, and can be visualised as a directed acyclic graph (generally
termed a Hasse diagram in the context of partial orders). If all
statements in 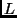 appear in the graph at some point, and are transitively
reachable from the most-general clause
appear in the graph at some point, and are transitively
reachable from the most-general clause  , then the refinement operator
is termed complete for the language
, then the refinement operator
is termed complete for the language 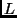 .
.
Shapiro proves the existence of a refinement operator complete for any first
order language in [Sha81]. This property in itself is not
particularly desirable, however, as it leads to inefficient induction of
theories due to the exponential explosion of the size of the refinement
graph. It is more interesting to define refinement operators that work on
subsets of 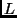 that are more likely to contain satisfactory theories, as
this is the only way the search is going to be tractable.
that are more likely to contain satisfactory theories, as
this is the only way the search is going to be tractable.
One class of interesting logic programs that can be enumerated via a
refinement operator in practice is the that of the definite clause
grammars. Using such an operator, it is possible to learn the syntax of
simple programming languages.
The refinement operator used in Section 4 is defined as follows:
Let 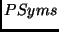 be the set of predicate symbols in
be the set of predicate symbols in 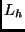 ,
,  the function
symbols; then
the function
symbols; then 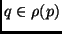 iff
iff 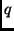 is a modification of
is a modification of 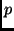 in precisely
one of the following ways:
in precisely
one of the following ways:
- Let
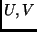 be distinct variables in
be distinct variables in 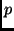 ; unify them in
; unify them in 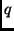 (i.e.
(i.e.
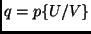 , read as ``substitute
, read as ``substitute 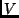 for
for 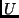 in
in 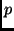 '').
'').
- Let
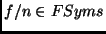 and
and 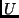 be a variable in
be a variable in 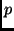 ; let
; let
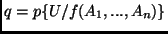 where the
where the 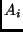 are new variables.
are new variables.
- Let
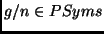 ,
, 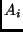 distinct variables in
distinct variables in 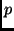 and
and
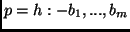 ; let
; let
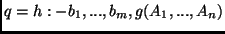 .
.
See Section 4.1 for a discussion of some of the
pragmatic issues of defining a useful refinement operator.
Figures 3 and 4 show how the two
clauses for the add/3 relation can be derived using these rules.
Note that in practice there will probably be several other clauses included
in the theory, such as the symmetric base case add(B, z, B).
Figure 3:
The success path through the refinement DAG for the base clause of add/3.
|
|
Figure 4:
The success path through the refinement DAG for the recursive clause of add/3.
|
|
Using Refinement Operators
In essence, the bug-correction algorithm employed by MIS is little more than
a search through an enumeration of all clauses in 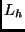 . Given the
intractability of this search in general, the given refinement operator
. Given the
intractability of this search in general, the given refinement operator
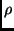 is used to bias the enumeration towards clauses that are more likely
to be correct.
is used to bias the enumeration towards clauses that are more likely
to be correct.
The search itself is general-to-specific, starting with the empty
theory  . The advantage of this strategy over a
specific-to-general one is that there is a simple starting point; for
the latter the initial theory would have to contain - notionally, at least
- all ground statements in
. The advantage of this strategy over a
specific-to-general one is that there is a simple starting point; for
the latter the initial theory would have to contain - notionally, at least
- all ground statements in 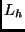 . This set will be infinite if there is at
least one function symbol with an arity of one or more in the language
(which will be the case in all interesting domains), and so is difficult to
represent on a physical machine.
. This set will be infinite if there is at
least one function symbol with an arity of one or more in the language
(which will be the case in all interesting domains), and so is difficult to
represent on a physical machine.
As 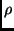 induces a partial (and not total) order on
induces a partial (and not total) order on 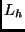 , three sets need
to be maintained:
, three sets need
to be maintained:
- The theory set contains all clauses that have been examined and
found to be consistent with the facts.
- The marked set contains all clauses that have been flagged by
the contradiction backtracing algorithm as the culprits for the proof of a
negative observation, and have yet to be refined.
- The dead set contains all marked clauses that have been
refined.
The search itself is straightfoward: select the next marked clause, add it's
refinements to the theory and move it to the dead set. Note that the
ordering of the marked set must be fair, for otherwise the algorithm
may get stuck examining an infinite path that does not contain useful
clauses. This is analogous to a Prolog proof attempt failing to terminate
even though the query logically follows from the program, due to it's
incomplete depth-first-search strategy.
In the context of Figure 1, searching the refinement DAG is
purely a generalisation step; the consistency of the resulting theory with
the facts is established by the framework itself.



Next: Examples of MIS Learning
Up: COMP9417 Project Shapiro's Model
Previous: The Contradiction Backtracing Algorithm
Peter Gammie
2002-03-01
![\includegraphics[width=\textwidth * 9/10]{firstRule.eps}](img50.png)
![\includegraphics[width=\textwidth * 9/10]{secondRule.eps}](img51.png)